Midterm Exam: Review Guide
This page contains problems similar to those that will appear on the
Midterm Exam.
Part I -- Tuesday, 09 October 2018
1. Evaluate the definite and indefinite integrals.
|
a.) |
\(\displaystyle \int x^2e^{2x}\,dx\)
|
|
h.) |
\(\displaystyle \int_0^\pi e^{\cos t} \sin(2 t)\, dt \)
|
|
b.) |
\(\displaystyle \int \arccos(x) \,dx\)
|
|
i.) |
\(\displaystyle \int \tan^3\theta \sec^6\theta\, d\theta \)
|
|
c.) |
\(\displaystyle \int \ln(\sqrt{x}) \,dx\)
|
|
j.) |
\(\displaystyle \int \sin^2 x\cos^2 x\, dx \)
|
|
d.) |
\(\displaystyle \int e^\theta\sin\theta\, d\theta \)
|
|
k.) |
\(\displaystyle \int \frac{x^2}{\sqrt{81 - x^2}} \, dx \)
|
|
e.) |
\(\displaystyle \int_0^{2\pi} t\sin(t)\cos(t)\, dt\)
|
|
l.) |
\(\displaystyle \int_0^7 \sqrt{x^2 + 49}\, dx \)
|
|
f.) |
\(\displaystyle \int \frac{z}{\sqrt{z^2 - 9}} \, dz\)
|
|
m.) |
\(\displaystyle \int \frac{7t - 5}{t + 5} \, dt\)
|
|
g.) |
\(\displaystyle \int \frac{17}{(x - 1)(x + 1)^2}\, dx\)
|
|
n.) |
\(\displaystyle \int \frac{25}{v^3 - 8} \,dv\)
|
2. Determine whether the improper integrals are convergent or
divergent. If convergent, evaluate the integral.
|
a.) |
\(\displaystyle \int_8^9 \frac{x}{x-9} \,dx\)
|
|
c.) |
\(\displaystyle \int_1^\infty \frac{1}{t^2} \, dt \)
|
|
b.) |
\(\displaystyle \int_1^\infty \frac{\ln x}{x} \,dx\)
|
|
d.) |
\(\displaystyle \int_0^1 \frac{1}{t^2} \,dt \)
|
Part II -- 10 October 2018
3. Derive the formulas for \(\tfrac{d}{dx}\big[ \arcsin(x)\big]\)
and \(\tfrac{d}{dx}\big[ \arctan(x)\big]\).
4. Derive the formulas for \(y = \sinh^{-1}(x)\) and
\(\tfrac{d}{dx}\big[\sinh^{-1}(x)\big]\).
5. Find the area of the region bounded by the hyperbola
\(25x^2 - 4y^2 = 100\) and the line \(x = 3\).
6. Compute the area of a lune: the shaded region in the image below.
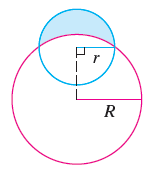
7.
Find the arc length of the curve \(y = \sqrt{2 - x^2}\), \(0 \leq x \leq 1\).
Check your answer by using geometry.
8.
Find the arc length function for the curve \(y = \arcsin(x) + \sqrt{1 - x^2}\)
with starting point \((0,1)\).
9.
Find the arc length function for the curve \(f(x) = \ln(\sin x)\), \(0 < x <
\pi\), with starting point \(\left(\frac{\pi}{2},0\right)\).
10.
Find the exact surface area of the surface obtained by rotating the curve about
the \(y\)-axis.
\[ y = \sqrt{1 + e^x}\, ,\ \ \ 0\leq x\leq 1 \]
11.
Compute the volume and surface area of Gabriel's Horn: the region obtained
by rotating the curve \(y = \dfrac{1}{x}\), \(x \geq 1\), about the \(x\)-axis.
Back to main page
Your use of Wichita State University content and this material is subject to our
Creative Common License.
