Midterm Exam: Review Guide
This page contains problems similar to those that will appear on the
Midterm Exam.
These questions are all similar to ones that you encountered while doing
your WebAssign homework.
1.
Find an equation of the plane through the points \(P(1,2,3)\),
\(Q(4,0,-1)\), and \(R(2,-4,-2)\).
2.
Find the distance between the point and the given plane.
\[\begin{cases}
P(1,-3,2) \\
\Pi:\ \ 3x + 2y + 6z = 5
\end{cases}\]
3.
Reduce the equation to one of the standard forms and classify the
surface.
\[x^2 - y^2 - z^2 - 4x - 2z +3 = 0\]
4.
You must be able to match the graph of a surface in \(\mathbb{R}^3\)
to its equation. (This will be a multiple choice question.)
5.
Consider the vector function
\[\mathbf{r}(t) = \dfrac{t^2-1}{t-1}\,\mathbf{i} +
\sqrt{t+8}\,\mathbf{j} + \dfrac{\sin \pi t}{\ln t}\,\mathbf{k}.\]
|
|
a.) |
What is the domain of \(\mathbf{r}\)?
|
|
|
b.) |
Compute \(\displaystyle \lim_{t\to 1} \mathbf{r}(t)\), provided it exists.
|
|
|
c.) |
Compute \(\dot{\mathbf{r}}(t)\), provided it exists.
|
6.
Find a parametrization of the curve of intersection of the cylinder
\(x^2 + y^2 = 4\) and the surface \(z = xy\).
|
(Recall that "parametrization" is another name for a vector function whose
terminal points trace out the space curve.) |
7.
Let \(\mathbf{u}\) and \(\mathbf{v}\) be vector functions in
\(\mathbb{R}^3\). Prove the product rule for the dot product:
\[ \frac{d}{dt}\Big[ \mathbf{u}(t)\cdot\mathbf{v}(t)\Big] =
\dot{\mathbf{u}}(t)\cdot\mathbf{v}(t) + \mathbf{u}(t)\cdot\dot{\mathbf{v}}(t).\]
|
Hint. Write both \(\mathbf{u}\) and \(\mathbf{v}\) in coordinates. |
8.
Consider the vector function
\(\mathbf{r}(t) = \left\langle \arctan(t), 2e^{2t}, 8te^t\right\rangle.\)
Find the unit tangent vector \(\mathbf{T}(0)\).
9.
Find \(\mathbf{r}(t)\) if \(\dot{\mathbf{r}}(t) = \left\langle
t, e^t, te^t \right\rangle\) and \(\mathbf{r}(0) = \mathbf{i} + \mathbf{j} +
\mathbf{k}\).
10.
Reparametrize the plane curve
\[\mathbf{r}(t) = \left(\dfrac{2}{t^2-1} - 1\right)\,\mathbf{i} +
\dfrac{2t}{t^2+1}\,\mathbf{j}\]
with respect to arc length from the point \((1,0)\) in the direction of
increasing \(t\). Express the reparametrization in simplest form. What can you
deduce about the curve?
11.
Compute the curvature \(\kappa\) of the twisted cubic
\(\mathbf{r}(t) = \left\langle t, t^2, t^3 \right\rangle\) at the point
\(P(1,1,1)\).
12.
At what point on the curve \(x = t^3\), \(y = 3t\), \(z = t^4\)
is the normal plane parallel to the plane \(6x + 6y - 8z = 1\)?
|
Hint. The normal plane has normal vector \(\mathbf{T}\): it is spanned
by the normal and binormal vectors, \(\mathbf{N}\) and \(\mathbf{B}\). |
13.
Show that the osculating plane at every point on the curve
\(\mathbf{r}(t) = \left\langle t+2, 1 - t, \tfrac{1}{2}t^2 \right\rangle\)
is the same plane. What can you conclude about the curve?
14.
Let \(C\) be a smooth space curve with unit tangent vector field \(\mathbf{T}\).
Prove that \(\mathbf{T} \perp \dot{\mathbf{T}}\) for all \(t\) in the domain
of \(\mathbf{T}\).
15.
Prove that the curvature of a circle of radius \(a\) is constant,
\(\kappa = 1/a \).
16.
Show that the limit does not exist.
\[\lim_{(x,y)\to (0,0)}\ \dfrac{x^4 - 30y^2}{x^2 + 15y^2}\]
17.
Determine the signs of the partial derivatives for the function
\(f\) whose graph is show, at the point \((x_0,y_0)\).
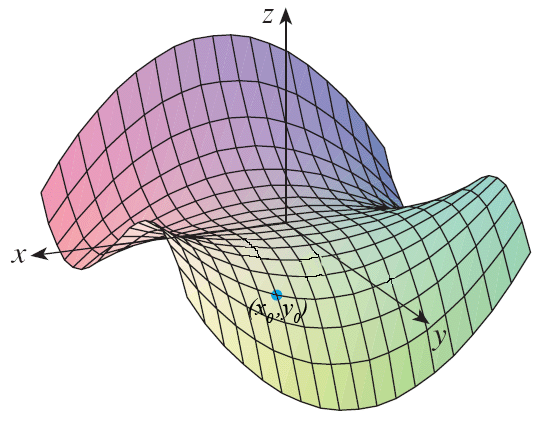
18.
Compute the second directional derivative \(D_{\mathbf{v}}^2 f(x,y)
= D_{\mathbf{v}}[D_{\mathbf{v}} f(x,y)]\)
for \(f(x,y) = x^3 + 5x^2y + y^3\) in the direction
of the vector \(\mathbf{v} = \langle 3,4 \rangle\) and evaluate it at the point
\((3,2)\).
19.
Consider the function \(f(x,y) = xy\) at the point \(P(6,5)\), and
consider the level curve \(f(x,y) = 30\). Find an equation of the tangent line
to the level curve at \(P\), and compute the gradient of \(f\) at \(P\). Then
show that the gradient vector is perpendicular to the level curve at \(P\).
20.
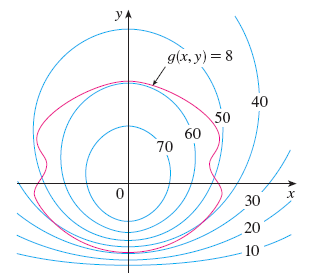
In the figure below, the blue level curves correspond to a function
\(f(x,y)\) and the red level curve corresponds to a constraint \(g(x,y) = 8\).
Estimate the maximum and minimum values of \(f\) subject to the constraint.
21.
Find the extreme values of the function \(f(x,y) = x^2 + y^2 + 4x - 4y\)
on the region \(x^2 + y^2 \leq 81\). [Hint: Use the method of Lagrange multipliers
on the boundary, and use the Second Derivative Test to check all critical points
in the interior.]
22.
Prove the theorem: Suppose \(f\) is a differentiable function of at
least 2 variables. The maximum value of the directional derivative
\(D_{\mathbf{u}}f(\mathbf{x})\) is \(\Vert\nabla f(\mathbf{x})\Vert\) and it occurs
when \(\mathbf{u}\) has the same direction as the gradient vector
\(\nabla f(\mathbf{x})\).
23.
Find an equation of the osculating circle to the curve \(y = 4x^2 - x^4\) at \(x = 2\).
24.
The involute of a space curve \(\mathbf{r}(t)\) is the space curve defined by
\(\ \mathcal{I}(t) = \mathbf{r}(t) - s(t)\mathbf{T}(t)\). Show that the involute of the helix,
\(\mathbf{r}(t) = \langle \cos t, \sin t, t \rangle\) lies in the \(xy\)-plane.
25.
Let \(f = f(x,y)\), \(x = r\cos\theta, y = r\sin\theta\), be a smooth function satisying
\[ \frac{\partial^2\, f}{\partial r^2} + \frac{1}{r} \frac{\partial\, f}{\partial r} +
\frac{1}{r^2} \frac{\partial^2\, f}{\partial\theta^2} = 0. \]
Show that
\[ \frac{\partial^2\, f}{\partial x^2} + \frac{\partial^2\, f}{\partial y^2} = 0. \]
Back to main page
Your use of Wichita State University content and this material is subject to our
Creative Common License.

