2. Show that the limit does not exist. \[\lim_{(x,y)\to (0,0)}\ \dfrac{x^4 - 30y^2}{x^2 + 15y^2}\]
3. Consider the function \(h(x,y) = g(f(x,y))\) where \(g(t) = t + \ln t\) and \(f(x,y) = \dfrac{4 - xy}{1 + x^2y^2}\). On what set is \(h\) continuous? Explain.
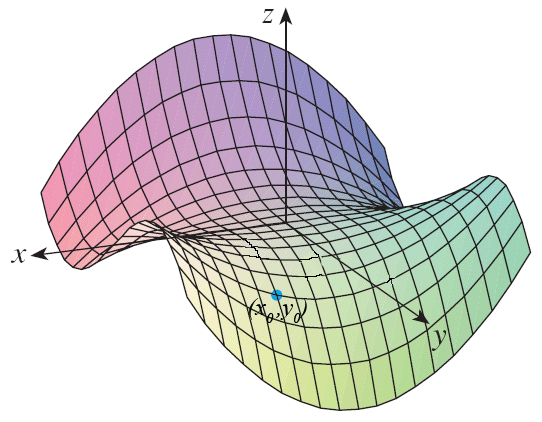
4. Determine the signs of the partial derivatives for the function \(f\) whose graph is show, at the point \((x_0,y_0)\).
5. Compute all second derivatives of the function \(f(x,y) = x^{9y}\).
6. A function \(u(x,y)\) is said to be harmonic if it obeys the second order differential equation \(\Delta u = 0\), where \[\Delta u = \dfrac{\partial^2 u}{\partial x^2} + \dfrac{\partial^2 u}{\partial y^2}.\] Supposing \( x(r,\theta) = r\cos\theta\) and \( y(r,\theta) = r\sin\theta\), use the chain rule to rewrite \(\Delta u = 0\) in terms of \(r\) and \(\theta\). [Hint: Solve for \(r\) and \(\theta\) as functions of \(x\) and \(y\).]
7. Compute the second directional derivative \(D_{\mathbf{v}}^2 f(x,y) = D_{\mathbf{v}}[D_{\mathbf{v}} f(x,y)]\) for \(f(x,y) = x^3 + 5x^2y + y^3\) in the direction of the vector \(\mathbf{v} = \langle 3,4 \rangle\) and evaluate it at the point \((3,2)\).
8. Consider the function \(f(x,y) = xy\) at the point \(P(6,5)\), and consider the level curve \(f(x,y) = 30\). Find an equation of the tangent line to the level curve at \(P\), and compute the gradient of \(f\) at \(P\). Then show that the gradient vector is perpendicular to the level curve at \(P\).
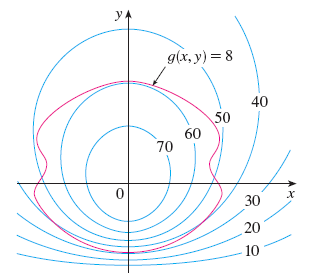
9. In the figure below, the blue level curves correspond to a function \(f(x,y)\) and the red level curve corresponds to a constraint \(g(x,y) = 8\). Estimate the maximum and minimum values of \(f\) subject to the constraint.
10. Find the extreme values of the function \(f(x,y) = x^2 + y^2 + 4x - 4y\) on the region \(x^2 + y^2 \leq 81\). [Hint: Use the method of Lagrange multipliers on the boundary, and use the Second Derivative Test to check all critical points in the interior.]
11. Prove the theorem: Suppose \(f\) is a differentiable function of at least 2 variables. The maximum value of the directional derivative \(D_{\mathbf{u}}f(\mathbf{x})\) is \(\Vert\nabla f(\mathbf{x})\Vert\) and it occurs when \(\mathbf{u}\) has the same direction as the gradient vector \(\nabla f(\mathbf{x})\).
12. Let \(\mathbf{x} = \langle x_1, x_2,..., x_n \rangle\) and \(\mathbf{y} = \langle y_1, y_2,.., y_n \rangle\).
a.) Find the maximum and minimum values of the dot product \(f(\mathbf{x},\mathbf{y}) = \mathbf{x}\cdot\mathbf{y}\) subject to the constraints \(\Vert\mathbf{x}\Vert = 1\) and \(\Vert\mathbf{y}\Vert = 1\).
b.) Set \(\mathbf{x} = \tfrac{\mathbf{a}}{\Vert\mathbf{a}\Vert}\) and \(\mathbf{y} = \tfrac{\mathbf{b}}{\Vert\mathbf{b}\Vert}\) for any vectors \(\mathbf{a}, \mathbf{b} \in \mathbb{R}^n\) and show that \[\vert\mathbf{a}\cdot\mathbf{b}\vert \leq \Vert\mathbf{a}\Vert\ \Vert\mathbf{b}\Vert.\] This is known as the Cauchy-Schwarz-Bunyachevsky Inequality.